문제
도넛과 막대 그래프
제출 내역
darklight
sublimevimemacs
Java
문제 설명
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프들이 있습니다. 이 그래프들은 1개 이상의 정점과, 정점들을 연결하는 단방향 간선으로 이루어져 있습니다.
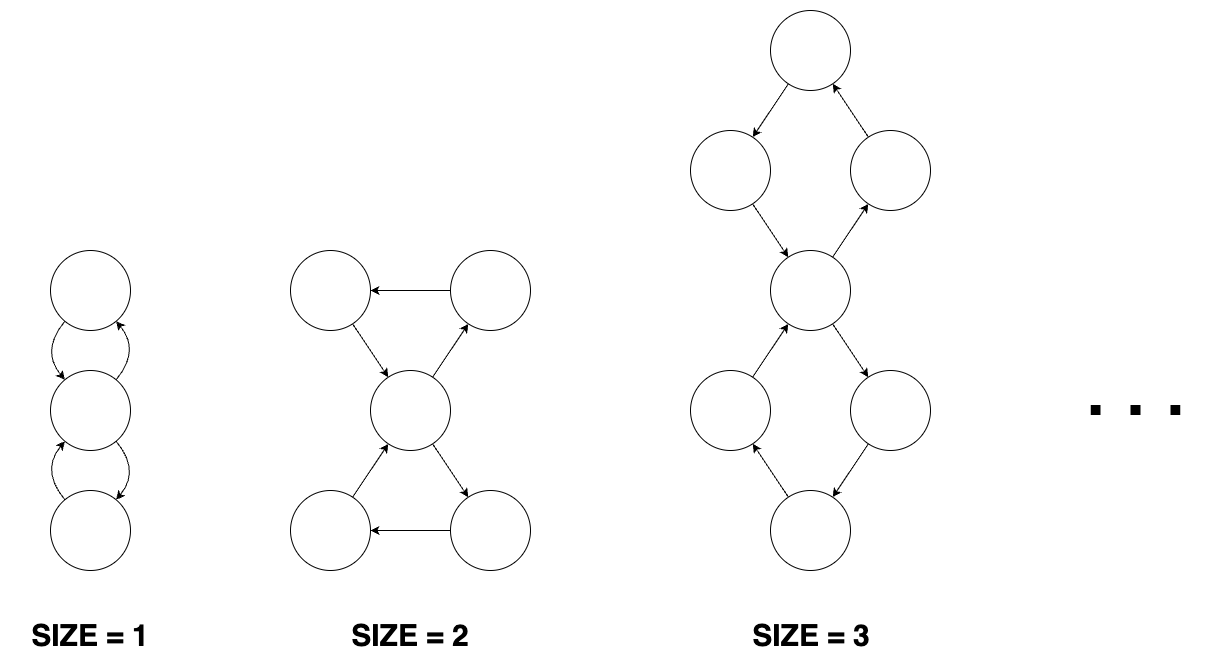
- 크기가 n인 도넛 모양 그래프는 n개의 정점과 n개의 간선이 있습니다. 도넛 모양 그래프의 아무 한 정점에서 출발해 이용한 적 없는 간선을 계속 따라가면 나머지 n1개의 정점들을 한 번씩 방문한 뒤 원래 출발했던 정점으로 돌아오게 됩니다. 도넛 모양 그래프의 형태는 다음과 같습니다.

- 크기가 n인 막대 모양 그래프는 n개의 정점과 n1개의 간선이 있습니다. 막대 모양 그래프는 임의의 한 정점에서 출발해 간선을 계속 따라가면 나머지 n1개의 정점을 한 번씩 방문하게 되는 정점이 단 하나 존재합니다. 막대 모양 그래프의 형태는 다음과 같습니다.

- 크기가 n인 8자 모양 그래프는 2n+1개의 정점과 2n+2개의 간선이 있습니다. 8자 모양 그래프는 크기가 동일한 2개의 도넛 모양 그래프에서 정점을 하나씩 골라 결합시킨 형태의 그래프입니다. 8자 모양 그래프의 형태는 다음과 같습니다.
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프가 여러 개 있습니다. 이 그래프들과 무관한 정점을 하나 생성한 뒤, 각 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 임의의 정점 하나로 향하는 간선들을 연결했습니다.
그 후 각 정점에 서로 다른 번호를 매겼습니다.
이때 당신은 그래프의 간선 정보가 주어지면 생성한 정점의 번호와 정점을 생성하기 전 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 구해야 합니다.
그래프의 간선 정보를 담은 2차원 정수 배열 edges가 매개변수로 주어집니다. 이때, 생성한 정점의 번호, 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 순서대로 1차원 정수 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤ edges의 길이 ≤ 1,000,000
- edges의 원소는 [a,b] 형태이며, a번 정점에서 b번 정점으로 향하는 간선이 있다는 것을 나타냅니다.
- 1 ≤ a, b ≤ 1,000,000
- 문제의 조건에 맞는 그래프가 주어집니다.
- 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.
입출력 예
edges result
| [[2, 3], [4, 3], [1, 1], [2, 1]] | [2, 1, 1, 0] |
| [[4, 11], [1, 12], [8, 3], [12, 7], [4, 2], [7, 11], [4, 8], [9, 6], [10, 11], [6, 10], [3, 5], [11, 1], [5, 3], [11, 9], [3, 8]] | [4, 0, 1, 2] |
입출력 예 설명
입출력 예 #1
주어진 그래프를 그림으로 나타내면 다음과 같습니다.
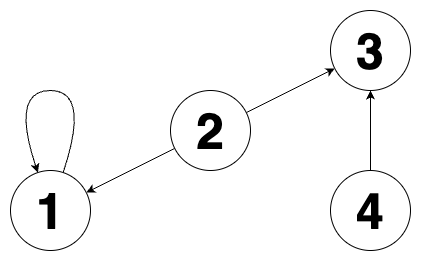
2번 정점이 생성한 정점이고 도넛 모양 그래프 1개, 막대 모양 그래프 1개가 존재합니다. 따라서 [2, 1, 1, 0]을 return 해야 합니다.
입출력 예 #2
주어진 그래프를 그림으로 나타내면 다음과 같습니다.
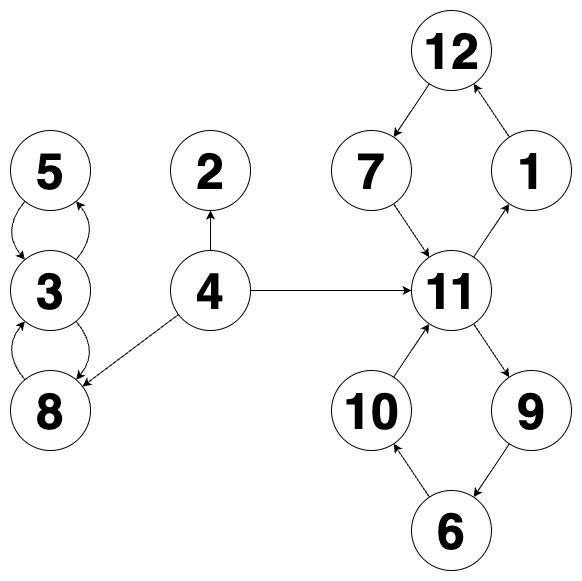
4번 정점이 생성한 정점이고 막대 모양 그래프 1개, 8자 모양 그래프 2개가 존재합니다. 따라서 [4, 0, 1, 2]를 return 해야 합니다.
※ 공지 - 2024년 1월 23일 테스트 케이스가 추가되었습니다. 기존에 제출한 코드가 통과하지 못할 수도 있습니다.
풀이
각 그래프의 특성을 명확하게 이해해야 한다. 또한, 모든 노드를 방문할 필요가 없는 문제였다.
각 노드의 특성은 이렇다.
임의의 중점
중점은 각 그래프를 연결하는 중간 점으로, 들어오는 간선이 없다는 특징이 있다. 이를 이용해 판별해주면 된다.
막대 그래프도 비슷한 특징이 있을 수 있지만, 문제에서 조건으로 최소 2개의 그래프가 존재한다 했으므로, 나가는 점이 최대 1개인 막대 그래프와 구별이 가능하다. 그러므로, 나가는 점이 2개 이상이며, 들어오는 점이 없는 점을 찾아주었다.
1. 도넛 모양 그래프
사이클이 존재하며, 막대와 8자의 특징을 섞어 놓았다. 나가는 간선과 들어오는 간선이 1개라는 점에서는 막대와 같지만, 사이클이 있다는 점에서는 8자와 같다.
Visited 배열을 통해 이미 방문한 경우 (사이클이 생기는 경우)를 찾았으나, 메모리와, 배열 처리를 하는 시간을 아낄 수 있는 방법이 있었다. 바로, 탐색 함수에 정점 노드와 이어진 시작 지점을 타겟 값으로 주어 탐색하는 노드가 시작 지점에 도착했다면 함수를 리턴해주는 방식을 사용하였다.
2. 막대 그래프
사이클이 존재하지 않는 유일한 그래프이며, 나가는 간선과 들어오는 간선이 1개이다. 가장 중요한 점은 언젠가 끝나는 지점이 있다는 것이다. 이 특성을 이용해 판별해주었다.
3. 8자 그래프
사이클이 존재하며, 나가는 간선과 들어오는 간선이 모두 2개인 경우가 하나라도 존재한다면 8자 모양 그래프라고 할 수 있다.
오류
9번 테스트 케이스가 계속 시간 초과가 났었다. 조금이라도 시간을 줄여보기 위해 get으로 그래프를 가져오는 방식을 바꾸다가 LinkedList의 get은 O(n)의 시간 복잡도가 있어 중점에 연결된 간선이 많고, 각 점이 가장 깊은 곳 까지 탐색한다면 get연산 만으로도 시간이 지연된다는 것을 발견하였다. 해결책으로는, LinkedList를 ArrayList로 복사하여 get연산시에 O(1)의 속도로 값을 찾을 수 있도록 바꿔주니 문제가 해결되었다.
코드
import java.util.LinkedList;
import java.util.List;
class Solution {
private static LinkedList<Integer>[] graph;
private static int[] incomingEdges;
static int[] answer = new int[4];
public static int[] solution(int[][] edges) {
int len = 0;
for (int[] edge : edges) {
len = Math.max(len, edge[0]);
len = Math.max(len, edge[1]);
}
incomingEdges = new int[len + 1];
graph = new LinkedList[len + 1];
// 그래프 초기화
initGraph(edges);
// 임의의 정점 찾기
int root = findCreateVertex();
answer[0] = root;
// 그래프의 사이즈 (이후에 2개의 그래프만 구해 전체에서 빼기 위해)
int graphSize = graph[root].size();
List<Integer> children = graph[root];
for (int cur : children) {
incomingEdges[cur]--;
findNode(cur, cur);
}
answer[1] = graphSize - answer[3] - answer[2];
return answer;
}
private static void initGraph(int[][] edges) {
for (int i = 0; i < graph.length; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : edges) {
graph[edge[0]].add(edge[1]);
incomingEdges[edge[1]]++;
}
}
// 임의의 정점은 나가는 간선이 2개 이상
// 들어오는 간선은 없음
private static int findCreateVertex() {
for (int i = 1; i < graph.length; i++) {
if (graph[i].size() >= 2 && incomingEdges[i] == 0) {
return i;
}
}
return 0;
}
// 8자, 1자 그래프 탐색
// 전체 그래프에서 뺄 두 개의 그래프를 8자와 1자로 한 이유는, 도넛의 경우 나가는 간선과 들어오는 간선이 2개이거나 1개인
// 경우 모두 성립하여 조건이 까다롭기 때문
// 막대 그래프는 마지막에 나가는 간선이 없음
// 잘라낸 그래프
// 11 2 8 재귀 탐색
private static void findNode(int node, int vis) {
int cur = 0;
if (graph[node].isEmpty()) {
answer[2]++;
return;
} else {
cur = graph[node].get(0);
if (graph[cur].size() == 2 && incomingEdges[cur] == 2) {
answer[3]++;
return;
} else if (vis == cur) {
return;
}
}
findNode(cur, vis);
}
}
'CodingTest' 카테고리의 다른 글
| 프로그래머스 코딩테스트 - 유연근무제 (0) | 2025.11.05 |
|---|---|
| 프로그래머스 3레벨 - 가장 긴 팰린드롬 (0) | 2025.06.01 |
| 코딩 테스트 입문 마무리 (0) | 2025.05.17 |
| 코딩테스트 입문 - Day 25 (0) | 2025.05.17 |
| 코딩테스트 입문 - Day 24 (0) | 2025.05.11 |
